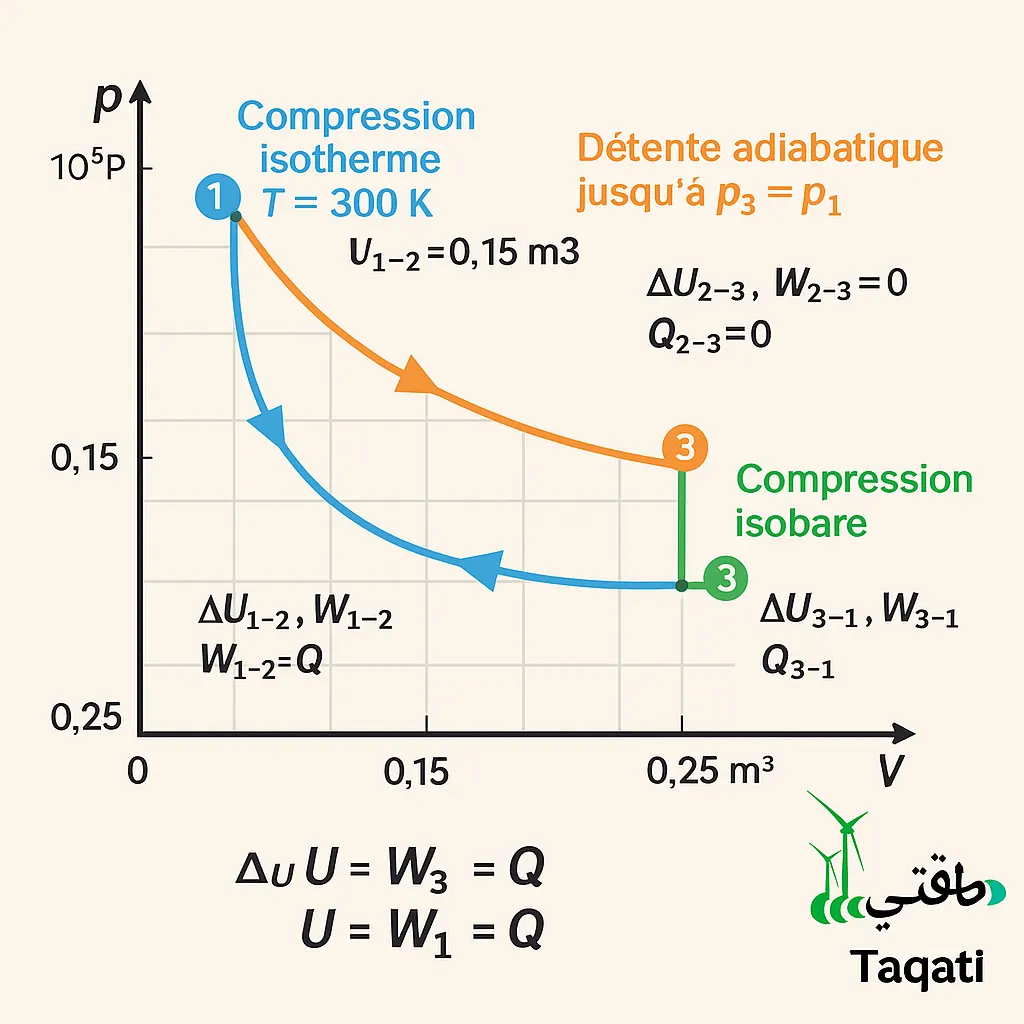
Analyse thermodynamique : cycle isotherme – adiabatique – isobare d’un gaz parfait :

1. Énoncé complet:

Un gaz parfait est initialement dans l’état 1 : température T₁ = 300 K, pression p₁ = 2,0 × 10⁵ Pa et volume V₁ = 0,25 m³. Il subit trois transformations réversibles successives :
• 1 → 2 : compression isotherme jusqu’au volume V₂ = 0,15 m³.
• 2 → 3 : détente adiabatique jusqu’à retrouver la pression p₃ = p₁.
• 3 → 1 : retour à l’état initial par une transformation isobare à p = p₁.

Constantes : R = 8,314 J·K⁻¹·mol⁻¹ ; γ = Cₚ/Cᵥ = 1,4.
Questions :

1. Déterminer la pression p₂ après l’isotherme et le volume V₃ après l’adiabatique.
2. Calculer pour chaque étape : variation d’énergie interne ΔU, travail W et chaleur Q.
3. Vérifier que l’énergie interne est une fonction d’état (ΔU sur le cycle = 0).

   2. Données et lois utilisées :

   

   
   

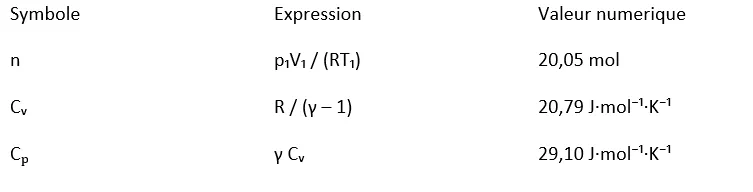
   Lois utilisées :

   
   

   · • Gaz parfait :

   
   

   pV = nRT

   
   

   · • Travail isotherme réversible :

   
   

   W = nRT ln(V₂/V₁)

   
   

   · • Relations adiabatiques réversibles :

   
   

   pV^γ = const ; TV^{γ-1} = const ; Q = 0

   
   

   · • Transformation isobare :

   
   

   W = nR ΔT ; Q = nCₚ ΔT ; ΔU = nCᵥ ΔT

   
   

   · • Premier principe :

   
   

   ΔU = Q - W (travail positif s’il est fourni par le système).

   
   

   3. Calcul des états 2 et 3 :

   
   

   • Pression après l’isotherme :

   
   

   p₂ = nRT₁ / V₂ = 3,33 × 10⁵ Pa.

   
   

   • Volume après l’adiabatique :

   
   

   V₃ = V₂ (p₂/p₁)^{1/γ} = 0,216 m³.

   
   

   • Température T₃ correspondante :

   
   

   T₃ = p₃V₃ / (nR) ≈ 259 K.

   
   

   4. Bilan énergétique par transformation:

   

   
   

   
   

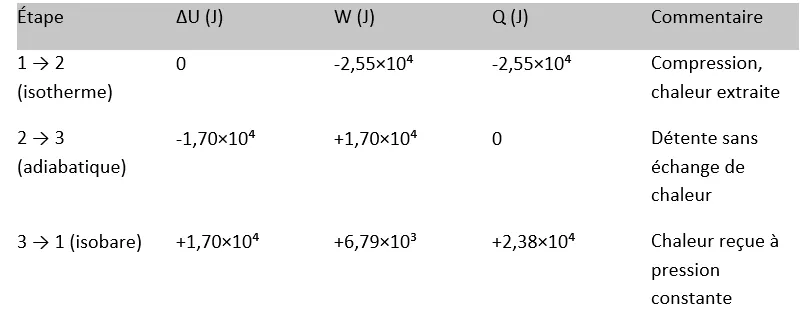
   On vérifie que ΣΔU = 0 et ΣQ = ΣW, conformément au premier principe pour un cycle.

   
   

   5. Réflexions pour approfondir la compréhension :

   
   

   · ❶ Choix du signe du travail : ici W > 0 lorsqu’il est fourni par le gaz (expansion). Bien définir la convention dès le départ évite les inversions de signe.

   
   

   · ❷ Lien entre équations différentielles et intégrales : la formule W = ∫p dV devient, pour l’isotherme d’un gaz parfait, nRT ln(V₂/V₁). Comprendre cette intégration aide à saisir la nature logarithmique du travail dans une compression lente.

   
   

   · ❸ Rôle du rapport γ: plus γ est grand, plus l’adiabatique s’écarte de l’isotherme. Cela se voit ici via l’exposant 1/γ dans V₃.

   
   

   · ❹ Fonction d’état : la démonstration ΔU_cycle = 0 illustre que l’énergie interne ne dépend que de l’état, pas du chemin. Refaire le même cycle dans l’ordre inverse donnerait les mêmes ΔU (signes opposés), alors que W et Q changeraient.

   
   

   · ❺ Diagramme p‑V : tracer le rectangle courbe (isotherme concave, adiabatique plus raide, isobare horizontale) permet de visualiser les aires (travail) et de vérifier la cohérence entre calcul analytique et géométrie.

   
   

   · ❻ Impact des arrondis: les petites différences (≈ 1,8 kJ) sur la somme des travaux & chaleurs proviennent des arrondis cumulés ; utiliser plus de chiffres significatifs ramène ΣQ + ΣW à zéro.

   
   

   · ❼ Extension : on pourrait calculer la variation d’entropie globale (qui doit être nulle pour un cycle réversible) pour consolider la maîtrise du second principe.

   
   

   6. Conclusion :

   
   

   L’exercice combine les trois transformations élémentaires pour mettre en œuvre les lois fondamentales de la thermodynamique. Il montre comment :

   
   

   • appliquer les relations gaz parfait + adiabatique ;

   • articuler premier principe et conventions de signe ;

   • démontrer la nature de fonction d’état de l’énergie interne.

   
   

   Ces raisonnements mathématiques et physiques sont transférables à tout cycle thermodynamique plus complexe.